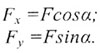Физика
| Скаляр - это величина, определяемая
только численным значением, например время t, масса m, путь l. |
| Действия с векторами |
| Сложение векторов |
| а) векторы направлены в одну сторону: |
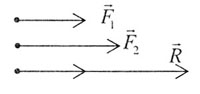 |
| Рис. 1 |
| б) векторы направлены в противоположные стороны: |
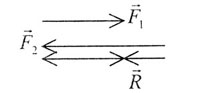 |
| Рис. 2 |
| в) векторы направлены под углом друг к другу: |
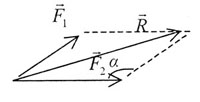 |
| Рис. 3 |
| Сложение осуществляется по правилу параллелограмма или треугольника. |
| В векторном виде результирующий вектор: |
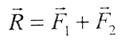 |
| в скалярном виде: |
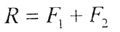 |
| в векторном виде: |
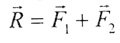 |
| в скалярном виде: |
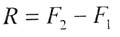 |
| В векторном виде результирующий вектор: |
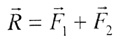 |
| В скалярном виде для нахождения R необходимо воспользоваться
теоремой косинусов. |
| Теорема косинусов: |
| квадрат стороны, лежащей против тупого угла, равен сумме
квадратов двух других сторон без удвоенного произведения этих сторон на
косинус угла,между ними: |
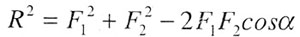 |
где 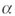 — тупой угол
между вектором — тупой угол
между вектором 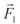 и перенесенным
в конец вектора и перенесенным
в конец вектора 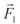 вектором вектором 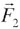 (рис. 3).
(рис. 3). |
В случае, если угол 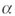 = 90°, cos
= 90°, cos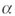 = 0 и теорема косинусов
превращается в теорему Пифагора: = 0 и теорема косинусов
превращается в теорему Пифагора: |
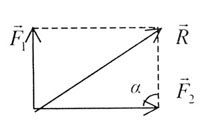 |
| Рис. 4. |
| Теорема Пифагора: |
| квадрат гипотенузы равен сумме квадратов катетов: |
 |
| Разложение вектора на составляющие |
| Осуществляется по правилу параллелограмма, в котором разлагаемый
вектор является диагональю, а результирующие векторы - сторонами: |
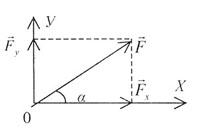 |
| Рис. 5 |
Разложение вектора 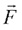 на составляющие по координатным осям X и У дает два вектора:
на составляющие по координатным осям X и У дает два вектора: 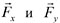 ,
модули которых: ,
модули которых: |
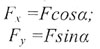 |
| Проекции векторов на оси |
| Проекции векторов на оси всегда скаляры: |
 |
| Рис. 6 |
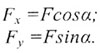 |
| Если направление вектора совпадает с направлением оси, проекция
положительна, если нет - отрицательна. |